The great physicist Lord Kelvin stated “To measure is to know” – a principle taken to heart by scientists across many disciplines. Not to be left out, computer scientists, since the earliest days of our discipline, have tried to come up with useful ways of measuring software. Cyclomatic complexity is one such metric, originally intended to measure a subprogram’s testability, maintainability, or understandability.
What is cyclomatic complexity?
Cyclomatic complexity (sometimes written v(G)) is a general graph-theoretic notion that, in software, can be applied to a subprogram’s control flow graph (CFG).
The definition is very simple and is as follows, where E is the number of edges in the CFG and N is the number of nodes:
v(G) = E – N + 2
So, in the example below, we have E=6 and N=6 so v(G)=2.
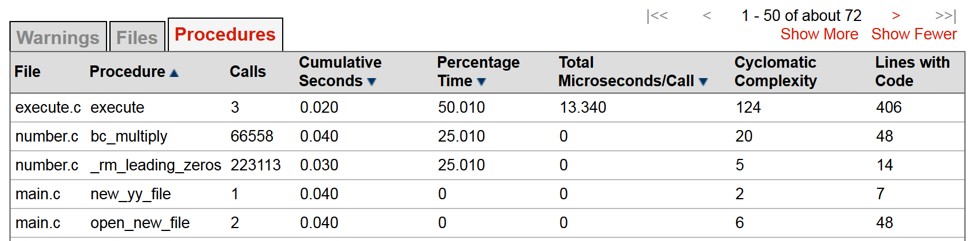
Using cyclomatic complexity for understandability
Cyclomatic complexity has made its way into various coding standards, where it is common to see recommendations that the value be kept at or below 10.
The intuition behind its use for understandability is that functions that employ a lot of branching are more difficult to comprehend than those that don’t, and v(G) captures the amount of branching nicely. (There are plenty of good arguments why this reasoning doesn’t always apply, but I won’t address that here.)
Instead, I’d like to point out that even though this is a very simple metric, a shocking number of tools are incapable of calculating it correctly, and organizations that ought know better are carelessly propagating a different definition that is just plain wrong.
Why is this worth your and my time? Because in a number of important uses, incorrect cyclomatic complexity values can be risky.
Hitting Close to Home
Our static analysis tool CodeSonar computes metrics, of course, and so I was concerned when I got an email from a prospect saying we were reporting the wrong value for cyclomatic complexity. The program model CodeSonar uses for each subprogram is essentially a control flow graph, so if we were getting v(G) wrong, then we could have had the wrong CFG in some cases, which could also mean failing to detect some instances of bugs.
So I asked for an example, and our prospect sent roughly the following:

They told me that CodeSonar was reporting v(G)=3, but the “correct” value should be 2.
At first glance, this code looks very much like the first example above (only one operator is different), so one might expect it to have the same cyclomatic complexity. However, if you draw out the CFG, as I’ve done below, it is easy to see where the misunderstanding is:
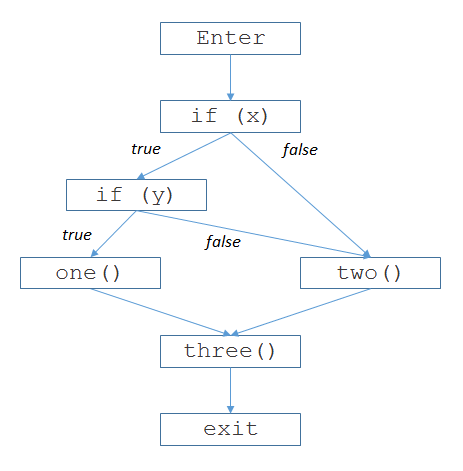
The difference is in the semantics of the logical and operator. In C, this operator is known as a short-circuiting operator; if the first operand is false, it does not evaluate the second operand because the result of the whole expression is going to be false. This isn’t much of a mystery, and every C programmer worth his or her salt knows this.
So I confirmed that CodeSonar was creating the correct CFG, and that it was computing the correct value of 3.
But why did my prospect think we were getting it wrong? As it turned out, their organization had been using a different tool to compute metrics for years, and as part of their evaluation of CodeSonar, they wanted to compare its values against those yielded by that other tool. It turned out that the root of the problem was that their older tool was simply getting it wrong.
I am going to be transparent here: The other tool was QA/C from Programming Research Ltd. (aka PRQA). I was somewhat surprised by this because that tool has been used fairly widely to compute code metrics by many different organizations. How could it get such a simple notion wrong?
Why did they get it wrong?
I decided to dig into this and I found a link to their manual. The documentation for cyclomatic complexity (for which they use the mnemonic STCYC), states that the value is the number of decisions in the function plus one. The last paragraph goes on to say “…some metrication (sic) tools include use of the ternary operator ? :…” (without stating whether they count it) and then “It could also be argued that the use of the && and || operators should be included.” This was the reason they were getting the wrong value — the short circuiting operators were simply being ignored.
Unfortunately, there is zero justification either in theory or practice for ignoring those operators. Admittedly, they are a little less obviously branches than the if or switch branches, but they are still unambiguously branches. If that code were rewritten to use a second if statement, then the CFG would be exactly isomorphic, but according to their definition, the value would be different.

Why is it OK to just make up new definitions for established terms? Electrical engineers don’t get to redefine what a volt is. Aeronautical engineers don’t use their own private definitions of thrust or lift. Doing so is like that famous eggy character in Lewis Carroll’s Through the Looking Glass:
‘When I use a word,’ Humpty Dumpty said in rather a scornful tone, ‘it means just what I choose it to mean – neither more nor less.’
Humpty Dumpty’s sentiment might be OK for literature, but certainly not for science or engineering.
I started wondering about other organizations whose tools compute cyclomatic complexity. As it turns out, PRQA are not the only folks in this boat. Klocwork also uses an incorrect definition, according to their manual.
A blog article from someone at Microsoft indicates that some versions of Visual Studio compute it incorrectly also, and he even states that the lowest value possible is 2, although it seems that this is because it counts implicit catch blocks.
But let me not just report on the bad news. I also discovered that Gmetrics gets it right, and Scitools does too.
But does this really matter?
It would be easy to imply that this doesn’t matter so much. As a predictive metric, cyclomatic complexity isn’t very good, so for many users of software metrics, the wrong value probably doesn’t matter very much because an approximate value is good enough, or because consistency is more important than precision. However, there is at least one very compelling reason why a value of v(G) that is too low might be dangerous.
Cyclomatic complexity yields a number that is a count of the number of linearly independent paths through a function, and so it provides the minimum number of test cases required to hit all combinations of decision points. For organizations that use this metric to tell them how many test cases to write, a low value may mean that they have too few cases, which could mean missing a serious problem in their code.
Finally, in safety-critical embedded development, large organizations (automobile manufacturers, for example) sometimes impose coding standards on their suppliers, and it is very common for those standards to include limitations on the cyclomatic complexity of individual functions. Suppliers may be unwittingly in violation of those standards if they are relying on tools that can’t count correctly.
So I would say yes, it matters.